How to make a Voxelised DNA Structure

DNA Structures are built from L-string seeded fractals.

L-strings and L-systems provide a grammar that can be used to generate a fractal. In this work, Hilbert curves are generated that are then converted into cubic placement ‘voxels’ for use in modelling.

import sys
from pathlib import Path

try:
    # The voxelisation library produces the cubic voxelisation that
    # can be used to build DNA
    from fractaldna.structure_models import voxelisation as v

    # The hilbert module produces and handles L-Strings
    from fractaldna.structure_models import hilbert as h
except (ImportError, ModuleNotFoundError):
    sys.path.append(str(Path.cwd().parent.parent.parent))
    from fractaldna.structure_models import voxelisation as v
    from fractaldna.structure_models import hilbert as h

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

Producing L-Strings

The hilbert model encodes a few basic fractals which can create Hilbert curves. These are

h.X: n<XFn<XFX-Fn>>XFX&F+>>XFX-F>X->
h.A: B-F+CFC+F-D&FnD-F+&&CFC+F+B<<
h.B: A&FnCFBnFnDnn-F-Dn|FnB|FCnFnA<<
h.C: |Dn|FnB-F+CnFnA&&FA&FnC+F+BnFnD<<
h.D: |CFB-F+B|FA&FnA&&FB-F+B|FC<<

Reference to these are all stored in hilbert.SUBSTITIONS.

The L-String language works as follows:

• interpret F as DrawForward(1);

• interpret + as Yaw(90);

• interpret - as Yaw(-90);

• interpret n as Pitch(90);

• interpret & as Pitch(-90);

• interpret > as Roll(90);

• interpret < as Roll(-90);

• interpret | as Yaw(180);

To ‘iterate’ an L-String, replace any reference to a subsititution with its value.

print("h.X:", h.X)
print("h.A:", h.A)
print("h.B:", h.B)
print("h.C:", h.C)
print("h.D:", h.D)

print("\nh.X iterated once:", h.iterate_lstring(h.X))

h.X: n<XFn<XFX-Fn>>XFX&F+>>XFX-F>X->
h.A: B-F+CFC+F-D&FnD-F+&&CFC+F+B<<
h.B: A&FnCFBnFnDnn-F-Dn|FnB|FCnFnA<<
h.C: |Dn|FnB-F+CnFnA&&FA&FnC+F+BnFnD<<
h.D: |CFB-F+B|FA&FnA&&FB-F+B|FC<<

h.X iterated once: n<n<XFn<XFX-Fn>>XFX&F+>>XFX-F>X->Fn<n<XFn<XFX-Fn>>XFX&F+>>XFX-F>X->Fn<XFn<XFX-Fn>>XFX&F+>>XFX-F>X->-Fn>>n<XFn<XFX-Fn>>XFX&F+>>XFX-F>X->Fn<XFn<XFX-Fn>>XFX&F+>>XFX-F>X->&F+>>n<XFn<XFX-Fn>>XFX&F+>>XFX-F>X->Fn<XFn<XFX-Fn>>XFX&F+>>XFX-F>X->-F>n<XFn<XFX-Fn>>XFX&F+>>XFX-F>X->->

Drawing Fractals

The function generate_path will generate a list of XYZ-points for a fractal L-String as below, which can then be plotted in matplotlib

print("Points seperated by 1 unit, no intermediate points")
print(h.generate_path("F", distance=1, n=1))
print("-")
print("Points seperated by 1 unit, 2 intermediate points")
print(h.generate_path("F", distance=1, n=2))

Points seperated by 1 unit, no intermediate points
[array([0, 0, 0]), array([1., 0., 0.])]
-
Points seperated by 1 unit, 2 intermediate points
[array([0, 0, 0]), array([0., 0., 0.]), array([1., 0., 0.])]

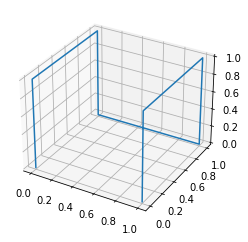
x_curve = np.array(h.generate_path(h.X, distance=1, n=10))

fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")

ax.plot(x_curve[:, 0], x_curve[:, 1], x_curve[:, 2])

[<mpl_toolkits.mplot3d.art3d.Line3D at 0x7fe943037c50>]

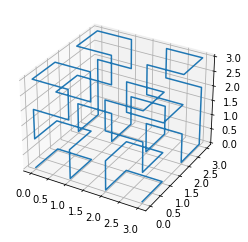
x_iterated = h.iterate_lstring(h.X)
x_curve2 = np.array(h.generate_path(x_iterated, distance=1, n=10))

fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")

ax.plot(x_curve2[:, 0], x_curve2[:, 1], x_curve2[:, 2])

[<mpl_toolkits.mplot3d.art3d.Line3D at 0x7fe9438b3c10>]

Making voxelised representations.

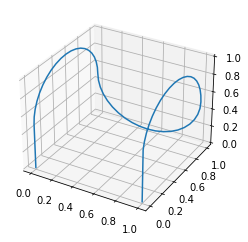
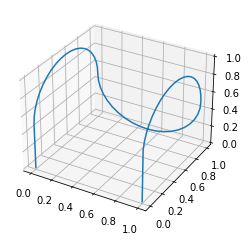
The voxelisation model can convert the path of this curve to a voxelised representation, of straight and curved boxes.

voxelised_fractal = v.VoxelisedFractal.fromLString(h.X)

# This can be plotted
voxelised_fractal.to_pretty_plot()

Exporting large-scale structures to text.

# And this can be returned as a data frame, or as text
voxelised_fractal.to_frame()

	IDX	KIND	POS_X	POS_Y	POS_Z	EUL_PSI	EUL_THETA	EUL_PHI
0	0	straight	0.0	0.0	0.0	0.000000	-0.000000	0.000000
1	1	turn	0.0	0.0	1.0	0.000000	-0.000000	1.570796
2	2	turn	-0.0	1.0	1.0	-1.570796	1.570796	0.000000
3	3	turntwist	-0.0	1.0	0.0	3.141593	-0.000000	0.000000
4	4	turn	1.0	1.0	-0.0	-3.141593	-1.570796	0.000000
5	5	turntwist	1.0	1.0	1.0	0.000000	-0.000000	-1.570796
6	6	turn	1.0	0.0	1.0	1.570796	1.570796	0.000000
7	7	straight	1.0	-0.0	0.0	3.141593	-0.000000	0.000000